Sayıların Dili, OYUN Mayıs 2007

Gizemli bir Üçgen

(Pascal Üçgeni)

Timur Karaçay

tkaracay@baskent.edu.tr

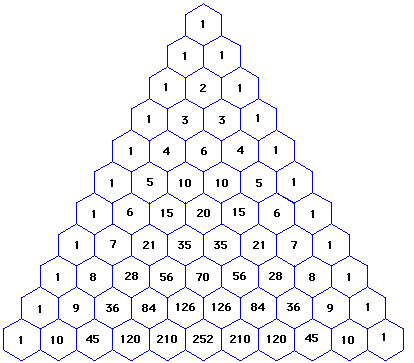
Şekil 1

1653 yılında yazmış olduğu bir kitap nedeniyle, batı literatüründe Ünlü Fransız düşünür ve matematikçi Blaise Pascal’a atfedilen bu gizemli üçgenin, Pascal’dan 700 yıl önce Çinliler tarafından bilindiği ortaya çıkmıştır. Yazık ki bilim tarihinde bu tür haksızlıklar çoktur. Bunun başka bir örneği de Tales Teoremidir. Tales’e maledilen teorem, Tales’den çok önce Babilliler tarafından biliniyordu. Ayrıca Tales’in Anadolu topraklarında (Milet) yaşadığını hiç söylemeyiz. Apollonius’un (Antalya) Perge’de, Aristo’nun (Çanakkale) Assos’ta yaşadığını okullarımızda öğretmeyiz. Oysa, Anadolu topraklarında yetişen ve uygarlıklara yön veren büyük düşünce insanlarına kucak açmak, bu topraklara ödememiz gereken bir borçtur.

Literatüre girdiği adla çağıracağımız Pascal üçgeni gerçekten gizemli özeliklere sahiptir. Bu özeliklerin bir kısmının elde edilişini birer zeka oyunu olarak görebiliriz. Ama onlar, oyun olmanın ötesinde cebir, geometri, olasılık, kaos gibi birbirleriyle ilişkisiz görünen bilim dallarında beklenmedik sonuçlar yaratmaktadır. Bu yazıda Pascal Üçgenini kuracak ve basit bazı özeliklerini söyleyeceğiz.

Pascal Üçgenini Oluşturmak

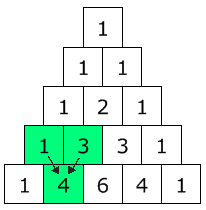
2.Şekil

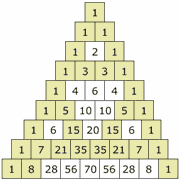
Pascal üçgenini oluşturmak çok kolaydır. 1.Şekilde görüldüğü gibi, bir eşkenar üçgenin tepesine 1 yazılır. Biraz sonra anlaşılacak bir nedenle, buna 0-ıncı satır diyelim. Bunun altına 1 , 1 sayılarını birinci satır olarak, gene şekildeki gibi yerleştirelim. İkinci satıra 1 , 2 , 1 ve üçüncü satıra 1 , 3 , 3 , 1 sayılarını yerleştirelim. Bu işleme durmaksızın devam edebilmek için, üçgene sayı yerleştirme kuralını çıkaralım. 1.Şekle dikkat edersek, herhangi bir satırı yerleştirirken uyulan kuralı hemen görebiliriz. Satırdaki her öğe, üst satırda kendisine göre sol üstünde ve sağ üstünde yer alan iki sayının toplamıdır ve o ikisinin konumlarına göre orta dikme üzerindedir (2.Şekil). Her satırın en solundaki ve en sağındaki sayılar daima 1 dir ve aynı kuralla bulunurlar. Sol kenar üzerindeki 1 lerin sol üst köşelerinde, sağdaki 1 lerin ise sağ üst köşelerinde sayı yoktur. Olmayan sayıları 0 sayarsak, genel kuralın kenardaki sayılar için de geçerli olduğu anlaşılır. Her satır ekleyişte yeni bir eşkenar üçgen ortaya çıkar. Bu işleme durmaksızın devam edebiliriz. Dolayısıyla, kenarlar sonsuz tane sayı içerecek kadar büyüyebilir. Ama her adımda bize sonlu tane sayı içeren bir eşkenar üçgen verir. O sonlu sayılar arasında harika ilişkiler ortaya çıkar.

Şimdi eşkenar üçgenimizin satırları ve köşegenleri üzerinde oynamaya başlayalım.

Pascal Üçgeni ve Cebir

Yatay satırlar, sırasıyla, ilköğretim aritmetik derslerinde gördüğünüz (x+y) iki terimlisinin kuvvetlerinin açılımındaki katsayılardır.

Kuvvet	Binom Açılımı	Pascal Üçgeni
0	(x+y)^0 = 1	1
1	(x+y)^1 = 1x + 1y	1, 1
2	(x + y)^2 = 1x^2 + 2xy + 1y^2	1, 2, 1
3	(x + y)^3 = 1x^3 + 3x^2 y+ 3xy^2 + 1y^3	1, 3, 3, 1
4	(x + y)^4 = 1x^4 + 4x^3 y+ 6x^2 y^2+ 4xy^3 + 1y^4	1, 4, 6, 4, 1
...	...	...

Bu sayılara Binom katsayıları denir. Olasılıkta ve kombinatorik hesaplamalarda önemli işlevleri vardır. Bu nedenle özel gösterimlere sahiptirler. Örneğin, dördüncü satırdaki binom katsayıları, sırasıyla, C(4,0)=1, C(4,1)=4, C(4,2)=6, C(4,3)=4 ve C(4,4)=1 simgeleriyle gösterilir. Kombinatorik hesaplamalara bir örnek olması için, şu basit problemi düşünelim. 4 arkadaş ikişer kişilik iki motorsikletle geziye çıkacaklar. Motorsikletlere kaç türlü binebilirler? Bu sorunun yanıtı, Pascal üçgeninin dördüncü satırındaki C(4,2)=6 sayısıdır. Buna, kombinatorik hesapta, 4 öğenin 2 şer 2 şer gruplanabilme sayısı denir. Genel olarak, n öğenin r-li gruplara ayrılabilme sayısı C(n,r) dir ve bu sayı (x+y)ⁿ binom açılımınındaki r-inci katsayıdır.

Satırların Toplamları

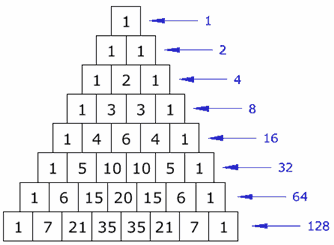
Satırların Toplamları Pascal üçgeninde bir satırın toplamı bir önceki satırın toplamının iki katıdır. Başka bir deyişle 2 nin kuvvetleridir:

3.Şekil

Pascal Üçgeni ve Geometri

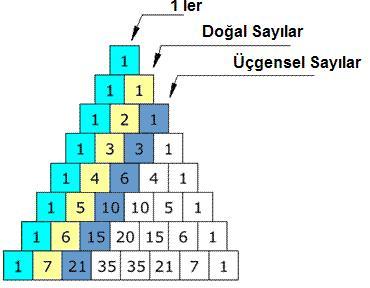
Köşegenler Sol kenara paralel köşegenleri düşünelim. Sol kenar “1” sayılarından oluşur. Ona paralel olan ilk köşegen üzerindeki sayılar 1,2,3,... doğal sayılarıdır. İkinci köşegen üzerindeki 1,3,6,10,15,21,... sayıları Üçgensel sayılardır. Üçüncü köşegen üzerindeki 1,4,10,20,35,... sayıları piramitsel (tetrahedral) sayılardır. Simetri nedeniyle, sağ köşegenler için de aynı şey söylenebilir.

4.Şekil

Pascal Üçgeni ve Fraktal Geometri

Sierpinki Üçgeni Pascal üçgeni içindeki tek ve çift sayıları farklı renklere boyarsanız, fraktal geometride ve kaos teorisinde rolü olan Sierpinki üçgeninin yapısına ulaşırsınız.

5.Şekil

Pascal Üçgeni ve Olasılık

Bir paranın her atılışında ya yazı (Y) ya da tura (T) gelecektir. Örnek olması için, bir parayı üç kez arka arkaya attığımızı varsayalım. Gelme olasılıkları neler olabilir? Üçü yazı gelebilir, üçü tura gelebilir ya da bazısı yazı bazısı tura gelebilir. Bütün olasılıkları sıralamak istersek, şöyle bir dizi oluşturabiliriz:

YYY, YYT, YTY, TYY, YTT, TYT, TTY, TTT

Tabii, atışlardan önce bu altı olasılıktan hangisinin geleceğini bilemeyiz. Ama üç atıştan sonra bu altı olasılıktan yalnızca birisinin gerçekleşeceğini kesinlikle biliriz. Bu, basitçe, bir olayın olma olasılığının hesabıdır. Bu tür konularla ilgilenen bilim dalına Olasılık Kuramı diyoruz. Olasılık Kuramı, çağdaş yönetim sistemlerinin, finans kurumlarının, ekonominin, haberleşme kuramının ve fizik biliminin önemli bir aracı haline gelmiştir.

Şimdi, olasılık ile Pascal Üçgeni arasındaki ilişkiyi görmek için, 1, 2, 3 ve 4 atışta paranın gelme olasılıklarını bir tabloda gösterelim.

En sağdaki sütuna bakarsak, oradaki sayıların Pascal Üçgenindeki sayılar olduğunu görüyoruz. Ayrıca, o sayılar kombinatorik hesapla ilgili sonuçları da söylüyor. Örneğin, paranın 4 atılışında, tam olarak, 2 tura (T) gelme olasılığı nedir? 4 atıştaki gelme olasılıkları sayısı, tablodan görüldüğü gibi, 1+4+6+4+1 = 16 (= 4x4) dır. Bunlar arasında yalnızca 6 tanesi iki tura (TT) içerir. O halde, 4 atışta tam olarak 2 tura gelme olasılığı 6/16 dır ki bu da %37,5 eder. Bunu binom katsayıları cinsinden yazarsak C(4,2) = 4!/(2!(4-2)! = 6 olur. Bu, yukarıda verdiğimiz motorsikletlere biniş örneği gibidir. Görüldüğü gibi, binom katsayıları görünüşte farklı nitelikteki problemlere çözüm getirmektedir.

Atış Sayısı	Gelme Olasılıkları	Pascal Üçgeni
1	Y T	1, 1
2	YY YT , TY TT	1, 2, 1
3	YYY YYT, YTY, TYY YTT, TYT, TTY TTT	1, 3, 3, 1
4	YYYY YYYT, YYTY, YTYY, TYYY YYTT, YTYT, YTTY, TYYT, TYTY, TTYY YTTT, TYTT, TTYT, TTTY TTTT	1, 4, 6, 4, 1
	...