Mantık, Matematik ve Felsefe III.Ulusal Sempozyumu

20-24 Eylül 2005, Foça

Çağrılı Konuşma

 

 

 

 

Genel Görelilik Kuramı

Timur Karaçay

Başkent Üniversitesi, Ankara

tkaracay@baskent.edu.tr

 

İçindekiler

• Antik Çağda Evren Modelleri
• Özel Görelilik Kuramı
• Genel Görelilik Kuramı

Fizik Yasaları Evrenseldir!

Newton hareket yasaları Maxwell’in elektrik ve magnetizma denklemlerine uymuyordu. Einstein, ortaya çıkan sorunu 1905 yılında ortaya koyduğu Özel Görelilik Kuramı ile giderdi:

Fizik yasaları bütün eylemsiz konuşlanma sistemlerinde aynıdır.

Özel Görelilik Kuramı, fizik yasalarını (Newton hareket yasaları, Maxwell elektromagnetizm yasaları) birbirlerine göre eylemsiz hareket eden iki cisim için bütünüyle çözmüştür. Başka bir deyişle, Özel Görelilik Kuramı, Newton Fiziğinin bir genellemesidir ve  bütün eylemsiz hareketleri kapsamıştır.

Eylemsiz hareket demek, düzgün doğrusal hareket demektir. Eylemsiz hareket ivmesizdir. İvmesiz hareket eden cisim, bir referans noktasına göre, ya bir doğru boyunca sabit bir hızla hareket eder ya da hareketsiz durur.

Öte yandan, doğada hareketlerin çoğunluğu eylemlidir, yani ivmeli hareketlerdir. Hızı ya da yönü değişen her hareket eylemli (ivmeli) dir. Örneğin, üzerinde yaşadığımız dünya eylemli hareket halindedir. Özel Görelilik Kuramı, fizik yasalarının eylemsiz konuşlanma sistemlerinde aynı olduğunu söyler söylemez akla takılan soru şudur:

Fizik yasaları birbirlerine göre eylemli (ivmeli) hareket eden iki cisim için geçerli değil midir?

Bunu biraz açıklığa kavuşturmalıyız.

Fiziğin hedefi en genel doğa yasalarını bulmaktır. Öyleyse, yalnızca eylemsiz konuşlanma sistemleriyle yetinilemez. Doğa yasaları eylemli konuşlanma sistemleri için de geçerli olmalıdır. Böyle olması fiziğe norm getirir, onu daha evrensel kılar. Özel Görelilik bu yönde değerli bir başlangıçtı ve mükemmel sonuçlar sunuyordu. Ama eylemsiz sistemlere kısıtlıydı.

Einstein, bu kısıtın kalkması gerektiğini sezinlemişti. Ona göre, fizik yasaları her yerde her koşul altında aynı olmalıydı. Sezgisel olarak ulaştığı bu sonucu matematik diliyle ifade etmesi gerektiğini de biliyordu. Olağanüstü zor olan bu iş onun tam on yılını aldı. 1915 yılında, ortaya koyduğu Genel Görelilik Kuramı fizik yasalarını önceden sezinlediği genel biçime koymuş oldu:

Fizik yasaları birbirlerine göre eylemli (ivmeli) hareket eden iki cisim için de geçerlidir.

Böylece, fizik yasalarının eylemli ve eylemsiz sistemlerde aynı olduğu gerçeği kanıtlanmış oluyordu. Bu olay, fiziğe bakış açımızı bütünüyle değiştirmiştir. Özetlersek, Özel Görelilik Kuramı, fizik yasalarının eylemsiz konuşlanma sistemlerinde aynı olduğunu söyler. Genel Görelilik Kuramı ise, bunu genelleştirir ve fizik yasalarının her sistemde (eylemli ya da eylemsiz) aynı olduğunu söyler.

Basitçe ifade ettiğimiz bu büyük bilimsel bulgunun dayandığı matematiğin anlatımı bir sömestrelik bir derstir. Bu konuşmada o uzun dersi yapamayacağımız için, temel matematiksel dayanakları betimlemekle yetineceğiz.

Sıradan Deneylerden Sıradışı Düşüncelere

Einstein, “damdan düşen bir adamın kendi ağırlığını hissetmeyeceğini” düşündüğü anı, hayatının en mutlu anı olarak niteler. Çünkü o anda, Einstein, Genel Görelilik Kuramına giden yolu görmüştür. Einstein’in düşüncelerini kavrayabilmek için basit deneylerden başlayacağız.

Bir avucunuza ağırca bir cisim (küçük bir taş parçası, madeni bir para vb.), öteki elinize daha hafif bir cisim (bir tahta parçası, plastik parçası vb.) alınız. Şimdi şu basit denemeleri yapınız.

·         İki elinizi havada dengeleyip, avuçlarınızdaki cisimlerden birinin daha ağır, ötekinin daha hafif olduğunu hissediniz.

·         İki avcunuzu yeterli çabuklukla yere doğru indiriniz. Avuçlarınızdaki cisimlerin ağırlıklarının, aynı oranlarda azaldığını hissedeceksiniz.

·         İki avcunuzu yere doğru biraz çabuk çekiniz. Avuçlarınızdaki cisimlerin ağırlıklarının yokolduğunu, ama cisimlerin avucunuzla birlikte yere doğru (ağırlıksız) indiğini hissedeceksiniz.

·         İki avcunuzu yere doğru daha çabuk çekiniz. Cisimlerin avuçlarınızdan ayrılıp havada kaldıklarını ve yere serbest düştüklerini göreceksiniz.

·         İki avcunuzu yeterli çabuklukla yukarı doğru kaldırınız. Avuçlarınızdaki cisimlerin ağırlıklarının arttığını hissedeceksiniz.

Bu yaptığınız deney, Genel Görelilik Kuramına temel olan düşünceleri açıklar. Şimdi, bunları Einstein’in düşsel asansörü ile açıklayalım.

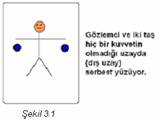
Her yanı kapalı bir asansörde bir gözlemci ve yanında iki taş bulunsun.

1.        Asansör hiç bir kuvvetin olmadığı dış uzayda (ağırlıksız ortam) serbest yüzüyorsa, gözlemci ve toplar hiçbir kuvvet etkisinde kalmazlar, asansörle birlikte serbest yüzerler (Şekil 3.1).

2.        Ağırlıksız ortamda, asansör bir iple yukarı doğru çekilsin. Bir ivme oluşur, Gözlemci ve taşlar asansörün tabanına düşerler. Asansördekiler, yukarı çekildiklerini fark edemez, gravitasyon[1] etkisi olduğunu sanırlar (Şekil 3.2).

   

3.                   Asansör ağırlıksız ortamdan çıksın ve gravitasyon alanına girsin. İpe asılı kalsın ama yukarı çekilmesin. Gözlemci ve taşlar (2) de olduğu gibi asansörün tabanına düşerler. Gözlemci yukarı çekilmekle, gravitasyon alanında olmak arasındaki farkı anlayamaz (Şekil 3.3). 

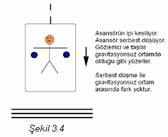
4.                   Gravitasyon alanında asılı duran asansörün ipi kesilsin. Gözlemci ve taşlar asansörle birlikte serbest düşmeye başlarlar. Gravitasyonsuz ortamda olduğu gibi yüzerler. Gözlemci gravitasyonsuz ortamda olmakla, gravitasyon alanında serbest düşme arasındaki farkı anlayamaz (Şekil 3.4).

             

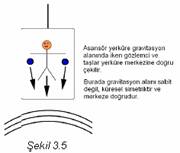
5.        Asansör yerküre gravitasyon alanında asılı dururken gözlemci ve taşlar yerküre merkezine doğru çekilir. Gözlemci yere doğru düşen taşların birbirlerine yaklaştığını fark eder (Şekil 3.5).

                      

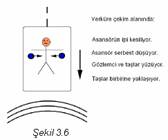
6.                   Yerküre gravitasyon alanında asılı duran asansörün ipi kesiliyor. Asansör serbest düşüyor. Gözlemci ve taşlar asansörde yüzmeye başlıyor. Gözlemci, taşların birbirlerine yaklaştığını görecektir (Şekil 3.6).

Yukarıda anlatılan düşsel asansör deneylerinden çıkarılacak sonuçlar şunlardır:

i)         İvmeli hareketle gravitasyon etkisiyle hareket arasındaki fark, yerel olarak, ayırt edilemez (1. ve 2. deney).

ii)       Gravitasyonun etkisi serbest düşmeyle, yerel olarak, yokedilebilir (3. ve 4. deney).

iii)      Düzgün olmayan bir gravitasyon alanında, yerel olarak, serbest düşmeye geçilerek gravitasyonun etkisi yokedilemez  (5. ve 6. deney).

Newton’un mutlak uzay varsayımı eylemsizlik ivmesine (direncine) ve merkezkaç kuvvetlere dayanır. Newton Mekaniği’nin, bir cismin m_g gravitasyon ivmesi ile m_i eylemsizlik ivmesini kuramsal açıdan farklı gördüğünü, ama Eötvös’ün 10⁸ de bir duyarlılıkla yaptığı deneylerde ikisi arasında pratik açıdan bir fark görülemediğini söylemiştik. Buna ek olarak, Galilei yasası uyarınca ağır ve hafif cisimler aynı hızla yere düşerler. Newton’un gök cisimleri arasındaki F=mMG/r² çekim kuvvetinden, çekim ivmesinin cismin m kütlesine bağlı olmadığını söylemiştik. Bütün bunlar bir arada düşünülünce, bu yasaların hepsini içine alan daha genel bir fizik yasasının varolduğunu düşünmek doğal olmaktadır. Einstein da böyle düşündü ve

Yerel olarak : Gravitasyon = Eylemsizlik = İvme

olduğunu gördü. Bu eşitlik çok şaşırtıcı değildir. İvmeyi ikinci basamaktan türev belirliyor. Eylemsizlik cismin düzgün hareketinin (dingin de olabilir) değişmesini engellemeye çalışan kuvvettir. Düzgün hareketin değişmesi demek, cismin ivme kazanması demektir. O halde, eylemsizlik kuvveti ivmeye karşı koyan bir kuvvettir. Etki-tepki yasası uyarınca eylemsizlik = ivme eşitliği doğal bir sonuçtur. Öte yandan, gravitasyonun etkisinin serbest düşmeyle (eylemsizlik), yerel olarak, yokedilebileceğini söylemiştik.

Eğri Uzay

Öklit Geometrisinde iki nokta arasındaki en kısa yolun  doğru[2] olduğunu öğretirler. Burada en kısa yol deyimi uzaklık kavramıyla ilgilidir. Öklit geometrisinde uzaklık bir metrik (fonksiyon) ile tanımlanır. P(x₁,y₁,z₁) ile Q(x₂,y₂,z₂)  noktaları arasındaki uzaklık (metrik)

bağıntısıyla verilir.

 

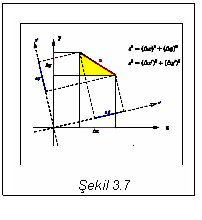Bilindiği gibi bu metrik katı dönüşümler altında değişmez. Katı dönüşüm deyiminden öteleme (paralel kayma) ve dönme dönüşümlerini anlıyoruz. Katı dönüşümler uzunluğu ve açıyı değiştirmez. Öklit geometrisinde geçerli olan bu kurallar başka geometrilerde başka biçimlere girebilir. Örneğin, Lizbon’dan Newyork’a gidecek gemi ya da uçak, en kısa yoldan gitmek isterse, iki kentten geçen paralel daireyi izlemez. Kaptanlar bu iki kentten geçen büyük çember üzerinde giderler. Bu nedenle, yolcular önce kuzeye doğru çıkıldığı sonra güneye doğru inildiği izlenimini edinirler. Çünkü, küre üzerindeki P noktasından bir Q noktasına giden en kısa yol  P ve Q dan geçen büyük çember yayıdır[3]. Öklit uzayındaki   doğrusunun yerini kürede  büyük çember yayı almıştır (Şekil 3.8). Başka yüzeylerde başka biçimler alacaktır. Örneğin, silindir yüzeyinde başka, hiperboloid yüzeyinde başkadır. (Görelilikte kullanılan terimlere uyum sağlamak için, Öklit uzayına düz uzay – flat space- , Öklit dışı uzaylara da eğri uzay –curved space- diyeceğiz.) 

 

                                               

 

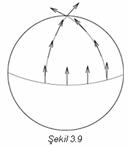
Öklit uzayında bir vektörü, kendisine paralel olarak, kapalı bir eğri boyunca kaydırarak (öteleme) ilk noktaya kadar getiriniz. Vektörün orijinal vektörle çakıştığını göreceksiniz. Ama küre üzerinde bu özelik bozulur. Başka bir deyişle, küre üzerinde paralel kayma yola bağlı olarak değişir (Şekil 3.9). Bu özelikten yararlanarak, yüzeyin eğriliğini (curvature) hesaplarız (Şekil 3.10). Diferensiyel Geometri derslerinde, eğriliğin ikinci basamaktan türevle hesaplandığını anımsayınız. Öte yandan, fizik derslerinde, ivmenin de ikinci basamaktan türevle hesaplandığını gördünüz. Buradan, ivme ile eğrilik arasında bir ilişki kurulabileceği sezilmektedir. Öte yandan, gravitasyonun ivmeye eşit olduğunu söyledik. O halde, gravitasyon ile eğrilik arasında bir ilişki doğmaktadır. Bütün bu söylediklerimizin matematiksel kanıtı vardır. Kanıtlarına giremeyeceğimiz Genel Görelilik Kuramının matematiği bunu yapmaktadır.

Uzayzamanda her olayı bir nokta ile göstereceğiz. İşin içine zaman girdiği için, uzayzamanda iki nokta arasında Öklit geometrisindekine benzer bir uzaklıktan sözedemeyiz. Noktalar arasındaki uzaklık terimi yerine, iki olay arasındaki uzayzaman aralığı terimini kullanacağız. Buna göre, Dt süresi içinde uzay koordinatlarındaki değişim Dx , Dy , Dz  ise, uzayzaman aralığı aşağıdaki bağıntı ile tanımlanır:

Bu bağıntı Minkowski metriği diye bilinir. Öklit metriği negatif değer alamazdı. Ama Minkowski metriği negatif ve pozitif değerler alabileceği gibi, farklı olaylar (noktalar) için sıfır değerini bile alabilir. Burada c bir dönüşüm sabitidir ve pratikte onu ışık hızı olarak kabul edeceğiz. Bu metrikte önemli olan şey, fotonların c hızıyla gitmesinden çok, koordinat dönüşümleri altında uzayzaman aralığını değişmez kılan bir c sabitinin varlığıdır. Başka bir deyişle, (t,x,y,z) eylemsiz sisteminden (t’,x’,y’,z’) eylemsiz sistemine geçilirse aşağıdaki eşitliği sağlayan bir c sabiti vardır.

Matematikçiler Minkowski metriğini daha zarif yollarla tanımlamayı ve Görelilik Kuramını sağlam bir matematiksel yapı içine almayı severler. Bu yönde yapılanlar öğrenilmeye değecek zerafet ve çekiciliktedir. Halen aktif çalışma alanı olan Gauge Kuramı, String Kuramı gibi kuramlar, Einstein’in kullandığı tensör yerine başka matematiksel yapılar koymaktadır. Bunların her birisi bu konuşmaya sığmayacak büyüklüktedir. O nedenle, işin matematiğini yapmak yerine, Einstein’in yaptıklarını betimlemekle yetinmek zorundayız.

Tensör hesapta bir noktanın koordinatları alt indislerle değil üst indislerle gösterilir. İşlemlerde, bileşen sayıları onlarla sayılacak kadar çok olduğu için kısaltmalar kullanılır. Örneğin, uzayzamanda dört boyutlu bir noktayı (olayı) göstermek için grek üs kullanılır. Zaman boyutunu dışlayıp uzaydaki üç boyutu belirtmek istersek, grek üs değil, latin üs kullanacağız:

                       

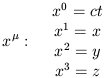
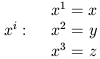
Uzayzaman aralığını daha kısa yazabilmek için, adına metrik denen

matrisini kullanacağız. Einstein basitliği seven bir insandı. Çok sayıda indisli terimlerin toplamını yazmak için kolay bir kısaltma önerdi. Aynı üs ya da indis taşıyan terimler bütün mümkün haller için toplanır. Buna göre, yukarıdaki uzunluk formülünü şu zarif biçimde yazabiliriz :

Uzayzamanda koordinat sistemlerimiz çok sık değişecektir. Koordinat sistemi değişince, yukarıda tanımlanan Minkowski metriğinin değişmez (invariant) kalmasını isteriz. O halde, uzayzamanda hangi dönüşümlerin metriği (uzunluğu) değiştirmediğini bilmeliyiz.  Bunu matris yardımıyla söylersek,

        ya da daha kısa olarak  

bağıntısını sağlayan  L matrislerini (dönüşümler) bilmeliyiz. Kolayca görüleceği gibi,

 

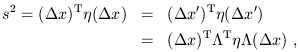
çıkar ve buradan   buluruz. Bu da    olması demektir. Bu eşitliği sağlayan matrislere Lorentz dönüşümleri denir. Lorentz dönüşümleri çarpma işlemine göre bir grup oluşturur. Poincaré, Lorentz dönüşümlerine ötelemeleri de ekleyerek daha genel dönüşüm grubunu oluşturmuştur. Her iki grup da komutatif değildir.

Minkowski Geometrisinin yapısını açıklayabilmek için tensör kavramına girmek gerekir ki biz ona giremeyeceğiz. Ama Genel Görelilik için matematiksel yapının nasıl kurulduğunu betimleyebiliriz.

Newton Mekaniği mutlak uzay ve mutlak zamanı varsaydığı için, kartezyen koordinat sistemi matematikte olduğu gibi Newton Mekaniğinde mükemmel bir araç olmaktadır. Fiziksel fenomenlerin çoğunu türev ve integral yardımıyla açıklarız. Uzayzamana bunu taşıyabilsek sorunlar çözülmüş olacaktı. Ama uzayzamanda bunu doğrudan yapamıyoruz.

Einstein, bu engeli aşabilmek için harika bir yol buldu. Düşüncesi, matematik analizde yaptığımız basit bir kavrama dayanıyordu. İvmeli hareket eden bir parçacığı düşünelim. Zaman dilimlerini durmadan küçültelim. Her adımda, zaman dilimlerinin uç noktaları arasındaki hız farkı giderek küçülecektir. Zaman dilimlerinin uzunluğunu sıfıra yaklaştıran sürecin (limit konumu) sonunda anlık hız ortaya çıkacaktır. Anlık hız sabittir, yani cisim ivmesizdir. Tam bu anda iken cismi bir eylemsiz konuşlanma sistemi içine koyabiliriz. Bunu yaptığımız anda Özel Görelilik Kuramının bütün sonuçlarını o an için uygulayabiliriz. Bu düşünceyle Einstein şu ilkeyi koydu

Einstein: Eşdeğerlik İlkesi

l       Keyfi bir gravitasyon alanındaki uzayzaman’ın her noktası için öyle yerel eylemsiz (serbest düşen) bir konuşlanma sistemi seçilebilir ki, noktanın yeterince küçük komşuluğunda doğa yasaları ivmesiz kartezyen koordinat sistemindeki biçimi (form) alır.

Tabii, burada ortaya şu sorun çıkıyor. İvmeli cisim için her an farklı bir hız vardır.  Öyleyse, her an için farklı bir eylemsiz konuşlanma sistemi olacaktır. O halde, bir sistemden ötekine dönüşümü kolayca yapacak bir yöntem gerekir. Açıktır ki bu bir matematiksel yapı içinde gerçekleşebilir. Einstein bu iş için tensörleri kullandı.

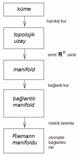
Matematikte hep yaptığımız gibi, konuyu önce eldeki nesnelerden arındırıp, yapıyı soyutlaştırmak işimizi kolaylaştıracaktır. Bir M kümesi düşünelim. Bu küme üzerine bir topolojik yapı koyalım. Sonra yerel olarak Rⁿ  Öklit uzayına benzetelim. Böylece M bir çokkatmanlı (manifold) olur. Sonra bir bağlantı (connection) kuralım, üzerinde bir metrik tanımlayalım. Böylece bir Riemann manifoldu elde edilir. Bu manifoldun her noktasına Öklit koordinat sistemleri iliştirilebilir ve bunlar arasında düzgün dönüşümler yapılabilir.

 

Şekil 3.11

Bundan sonrası uzun ve ciddi matematiksel işlemler gerektirir. Sonuçta Genel Görelilik Kuramı gravitasyonu uzayzamanın eğriliği olarak açıklar. Einstein alan denklemleri (field equations) tensörel biçimiyle çok yalın görünür. [Zaten Einstein bütün bulgularını böyle yalın biçimlerde vermiştir.]

Genel Göreliliğin tensör hesaba dayanan işlemlerinde sağdaki ve soldaki indislerin her birisinin dörder değeri olduğunu, dolayısıyla, yukarıda alan denklemleri dediğimiz eşitliğin 4x4x4x4=256 denklem içerdiğini söylemek gerekir. Ancak, simetriler nedeniyle denklem sayısı 10’a düşer. Einstein bu denklemlerin uzun süre çözülemeyeceğini sanıyordu. Ama, Schwarzchild bir yıl geçmeden bir çözüm buldu. Halen, farklı parametrelerle çözüm arayan araştırmacılara raslayabilirsiniz.   

Özel ve genel görelilik Kuramları Arasındaki Önemli Farklar:

1.                   Özel Görelilik Kuramında mutlak hız’dan sözedemeyiz. Ancak, eylemsiz sistemlere göreli hız’dan sözedebiliriz. Bunun nedeni, hızların 4-boyutlu uzayzamanda birer vektör olarak temsil edilmesidir. Bir eylemsiz sistemden ötekine geçildiğinde hız vektörünün yönü değişecektir. 

Özel Görelilik Kuramında ise, uzayzamanın aynı noktasında olmayan cisimlerin göreli hızlarından bile sözedemeyiz. İki cismin, uzayzamanın aynı noktasında olmaları demek, aynı yerde aynı zamanda (eşanlı) olmaları demektir. Farklı noktalardaki cisimlerin hızlarını karşılaştırmak istediğimizde, önümüze olanaksız bir durum çıkar. Çünkü, bir vektörü başka bir vektörle karşılaştırmak için birisini kendisine paralel kaydırarak (öteleme) ötekinin üstüne çakışıp çakışmadığına bakmak gerekir. Oysa eğri uzayda paralel kayma yola bağlıdır. Dolayısıyla, farklı noktalardaki iki cismin hızları karşılaştırılamaz. 

2.                   Özel Görelilik Kuramında bir eylemsiz koordinat sistemini, her biri ötekine göre dingin (hareketsiz) duran saatlerin (vektör) alanı gibi düşünebiliriz.

Genel Görelilik Kuramında böyle bir düşünceye yer yoktur. Ancak aynı noktada olan saatlerin göreli hızlarını karşılaştırabiliriz. Başka bir deyişle, fizikte çok önemli rolü olan eylemsiz sistemler genel görelilikte yoktur.

3.                   Fizik yasalarını eylemsiz sistemlerdeki nitelikleriyle Genel Görelilikte de kullanmak istiyoruz. O nedenle, yerel olarak eylemsiz sistemleri uzayzamana yerleştiriyoruz. Burada yerel terimi önemlidir. Bu işi ancak uzayzaman aralığının sıfıra gittiği limit halde yapabiliriz. Başka bir deyişle, iki cismin anlık hızlarını karşılaştırabiliriz.

4.                   Bir parçacık gravitasyondan başka bir etki altında değilse, ona serbest düşüyor denilir. Bir  “test parçacığı”  deyince enerjisi ve momentumu çok küçük olduğu için uzayzaman eğriliğine etki etmeyen bir cismi anlayacağız. Genel görelilikte, serbest düşen bir test parçacığının yörüngesi bir jeodeziktir. Bunun hız vektörü ise jeodezi boyunca paralel kayan teğet vektördür.

5.                   Genel Görelilik Kuramında gravitasyon geröek bir kuvvet değildir. O uzayzamanın eğriliğinin ortaya koyduğu bir fenomendir. [Dikkat: uzayın eğriliği değil, uzayzamanın eğriliği]. 

 

KAYNAKLAR

Özel ve Genel Görelilik Kuramını anlatan çok sayıda kaynak vardır. Bu büyük çeşitlilik içinde çok iyi kitaplar yanında, çok kötü yazılmış olanlar da vardır. Bu arada çok kötü çeviriler de görebilirsiniz. İnternette sayısız kaynağa erişilebilmektedir. Bunların da bazıları özenle hazırlanmış yararlı kaynaklardır. Ortaya konuluşundan bu yana yüz yılı aşan bu kuramı anlatmak için söylenmemiş söz, verilmemiş örnek, çizilmemiş diyagram kaldığını sanmıyorum. Örnekler ve diyagramlar artık anonimdir. Thales teoremine kaynak göstermek ne anlam taşırsa, bu yazıya kaynak göstermek de o anlamı taşıyacaktır. Kaynak yerine, bu metnin orijinal olmadığını, anonimden derlemeler olduğunu söylemek daha doğru olacaktır.